Students understand mathematics in many complex ways.  Students ask questions, see ideas, draw representations, connect methods, justify, and reason in all sorts of different ways.  But recent years have seen all of these different nuanced complexities of student understanding reduced to single numbers and letters that are used to judge students’ worth.  Teachers are encouraged to test and grade students, to a ridiculous and damaging degree; and students start to define themselves – and mathematics – in terms of letters and numbers.  Such crude representations of understanding not only fail to adequately describe children’s knowledge, in many cases they misrepresent it.

This chapter deals with the growth in standardised testing and that often in mathematics classes this practice is mimicked through the delivery of low-quality standardised tests.  This is despite the knowledge that these tests only assess a narrow focus within mathematics.

The testing regime of the last decade has had a large negative impact on students, but it does no end with testing; the communication of grades to students is similarly negative.  When students are given a percentage or grade, they do little else besides compare it to others around them, with half or more deciding that they are not as good as others.  Commonly students describe themselves by saying “I am an A student” or “I’m a D student”.

So this is where FEEDBACK comes into it…the reason it is in the top 10 of strategies to improve learning.

The students receiving comments (not grades) learned twice as fast as the control group, the achievement gap between male and female students disappeared, and student attitudes improved.

This is the response to a mathematics homework study where half the group were given grades and half the group were given diagnostic comments and no grades.

Race to Nowhere

An American documentary that addresses the stress upon today’s students:

Assessment for Learning

Paul Black and Dylan Wiliam provide some valuable insights into the use of assessment for learning.

Teachers who use A4L spend less time telling students their achievement and more time empowering student to take control of their learning pathways.

The 3 vital questions:

1. Where students are now
2. Where students need to be
3. Ways to close the gap

http://www.tandfonline.com/doi/pdf/10.1080/0969595980050102

https://weaeducation.typepad.co.uk/files/blackbox-1.pdf

Developing Student Self-Awareness and Responsibility

The most powerful learners are those who are reflective, who engage in metacognition – thinking about what they know – and who take control of their own learning.  A major failure of traditional mathematics classes is that students rarely have much idea of what they are learning or where they are in the broader learning landscape.  They focus on methods to remember but often do not even know what area of mathematics they are working on.

There are many strategies for encouraging students to become more aware of the mathematics they are learning and their place in the learning process.  Here are 9 favourites of the author of Mathematical Mindsets:

1. Self-Assessment
2. Peer Assessment
3. Reflective Time
4. Traffic Lighting (understand (green), partially understand (yellow) and need help (red) – some Teachers hand out coloured paper cups)
5. Jigsaw Groups (work together to become experts on a particular area and then split and join new groups to share information)
6. Exit Tickets
7. Online Forms
8. Doodling
9. Students write questions and tests

Advice on Grading

Many teachers, unfortunately, are forced into grading, as it is a requirement of their school district or the administrators of their school.  The following lists compiles advice on ways to grade fairly and to continue communicating positive growth messages even when faced with a grading requirements:

1. Always allow students to resubmit any work or test for a higher grade;
2. Share grades with school administrators but not with the students;
3. Use multidimensional grading
4. Do not use a 100-point scale
5. Do not include early assignments from mathematics class in the end-of-class grade
6. Do not include homework, if given, as any part of grading

Not all practical but worth thinking about and discussing at another time.  Some of our feedback work should be designed to provide students with opportunities to improve on drafts and early tests.

 

Tracking is a process often used in many schools in United States where students are placed into tracked groups in seventh grade.  These separate classes provide higher- or lower-level content to students.

Opportunities to Learn

One key factor in student achievement is known as “opportunity to learn” (OTL).  Put simply, if students spend time in classes where they are given access to high-level content, they achieve at higher levels.

We cannot know what a 4- or 14 year old is capable of, and the very best environments we can give to students are those in which they can learn high-level content and in which their interest can be piqued and nurtured, with teachers who are ready to recognize, cultivate and develop their potential at any time.

Teaching Heterogeneous Groups Effectively: The Mathematics Tasks

1. Providing Open-Ended Tasks
2. Offering a Choice of Tasks
3. Individualised Pathways (SMILE – http://www.nationalstemcentre.org.uk/elibrary/collection/44/smile-cards)

Teaching Heterogeneous Groups Effectively: Complex Instruction

Experienced teachers know that group work can fail when students participate unequally in groups.  If students are left to their own devices and they are not encouraged to develop productive norms, this is fairly likely to happen: some students will do most of the work, some will sit back and relax, some may be left out of the work because they do not have the social status with other students.

https://www.youcubed.org/category/making-group-work-equal/

Multidimensionality

In complex instruction (CI) classrooms, teachers value, and assess students on, the many different dimensions of mathematics.  The mantra of the CI approach:

No one is good at all of these ways of working, but everyone is good at some of them

When students were interviewed in traditional mathematics classrooms as part of the study in the US, they were asked: “What does it take to be successful in mathematics?” A stunning 97% of students said the same thing: “Pay careful attention.” This is a passive learning act that is associated with low achievement (Bransford, Brown, & Cocking, 1999).  At the CI classroom when students were asked the same question they came up with a range of ways of working, such as:

• Asking good questions
• Rephrasing problems
• Explaining
• Using logic
• Justifying methods
• Using manipulatives
• Connecting ideas
• Helping others

Students when faced with mathematics problems are encouraged to read questions out loud, and when they are stuck, to ask each other questions such as:

• What is the question asking us?
• How could we rephrase this question?
• What are the key parts of the problem?

The students’ engagement was due to many factors:

• The work of the teacher, who had carefully set up the problem and circulated around the room asking students questions
• The task itself, which was sufficiently open and challenging to allow different students to contribute ideas
• The multidimensionality of the classroom: different ways to work mathematically, such as asking questions, drawing diagrams, and making conjectures were valued and encouraged
• The request to deal with a real-world object or idea
• The high levels of communication among students who had learned to support each other by asking each other questions.

Assigning Competence

Teaching students to be responsible for each other’s learning

Roles

For mathematics can, on the one hand, be though of as an incredible lens through which to view the world; an important knowledge, available to all, that promotes empowered young people ready to think quantitatively about their work and lives and that is equitably available to all students through study and hard work.  On the other hand, mathematics can be thought of as a subject that separates children into those who can and those who cannot, and that is valuable as a sorting mechanism, allowing people to label some children as smart and others as not smart.

The Myth of the Mathematically Gifted Child

Some people, including some teachers, have built their identity on the idea they could do well in maths because they were special, genetically gifted in mathematics, and the whole “gifted” movement in the United States is built upon such notions.  But we have a great deal of evidence that although people are born with brain differences, such differences are eclipsed by the experiences people have during their lives, as every second presents opportunities for incredible brain growth. (Thompson, 2014; Wo0llett & Macquire, 2011)

Equitable Strategies

1. Offer all students high-level content
2. Work to change ideas about who can achieve in mathematics
3. Encourage students to think deeply about mathematics
4. Teach students to work together
5. Give all students encouragement to learn maths and science
6. Eliminate (or at least change the nature of) homework

Teachers are the most important resource for students.  They are the ones who can create exciting mathematics environments, give students the positive messages they need, and take any math’s task and make it one that piques students’ curiosity and interest.

Interestingly, I found that mathematics excitement looks exactly the same for struggling 11-year-olds as it does for high-flying students in top universities – it combines curiosity, connection making, challenge, and creativity, and usually involves collaboration.  These, for me, are the 5 C’s of mathematics engagement.

Boaler, Mathematical Mindsets

5 cases of true mathematics excitement (This is just an overview of those cases.  What is valuable and probably can’t be conveyed in this blog post is the discussions that occurred during these tasks.)

Case 1. Seeing the Openness of Numbers

With a Silicon Valley start-up group that were looking to develop an online mathematics course the author when asked to what makes a good maths question, they stopped the conversation and asked the group if they could ask them all a math question.  The author enacted a mini version of a number talk.  They asked everyone to think about the answer to 18 X 5 and to show her, with a silent thumbs-up, when they had an answer.  The team then shared their methods and there were at least six different methods.  The author drew them up visually.  It was the sharing and discussion around these methods that created the engagement and excitement in understanding that there were so many ways to think about an abstract number problem.

Mathematics is a subject that allows for precise thinking, but when that precise thinking is combined with creativity, flexibility, and multiplicity of ideas, the mathematics comes alive for people. Teachers can create such mathematical excitement in classrooms, with any task, by asking students for the different ways they see and can solve tasks and by encouraging discussion of different ways of seeing problems.

Case 2. Growing Shapes: The Power of Visualisation

 Middle School classroom in San Francisco Bay Area.  The focus was algebra, but not algebra as an end point, with students mindlessly solving for x.  Instead, algebra was taught as a problem-solving tool tha could be used to solve rich, engaging problems.  The students had just finished sixth and seventh grades, and most of them hated maths.  Approximately half the students had received a D or an F in their previous school year.

The task that created the case of mathematics excitement came from Ruth Parker; it asked students to extend the growing pattern shown below:

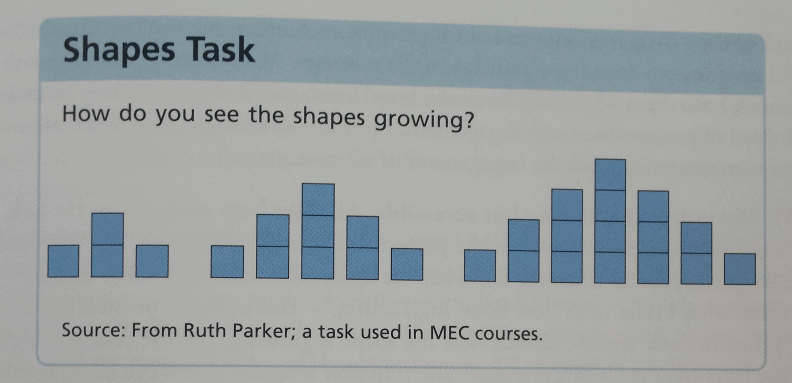
The success of the task was in the discussions particularly with a number of difficult boys and remained on task for 70 minutes.  Some of their work below:

Here are some important observations that reveal opportunities to improve the engagement of all students:

1. The task is challenging but accessible
2. The boys saw the task as a puzzle
3. The visual thinking about the growth of the task gave the boys understanding of the way the pattern grew
4. They had all developed their own way of seeing the pattern growth
5. The classroom had been set up to encourage students to propose ideas without being afraid of making mistakes
6. Taught the students to respect each other’s thinking
7. Using their own ideas
8. Working together
9. Boys were working heterogeneously

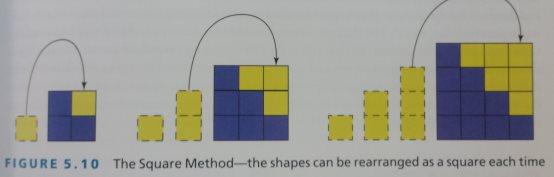
Another way of solving the problem that led to discussions about why the pattern was growing as a square, why it was (n + 1) squared.

 Case 3. A Time to Tell?

When I share open, inquiry-based mathematics tasks with teachers, such as the growing shapes or “raindrop” task just discussed, they often ask questions such as, “I get that these tasks are engaging and create good mathematical discussions, but how do students learn new knowledge, such as trig functions? Or how to factorize? They can’t discover it.”

The traditional approach has been Teachers show the method and then students use them.

Researchers have found that when students were given problems to solve, and they did not know methods to solve them, but they were given opportunity to explore the problems, became curious, and their brains were primed to learn new methods, sot that when Teachers taught the methods, students paid greater attention to them and were more motivated to learn them.

So the question is not about whether we should tell or explain methods but when is the most appropriate time.  The student showed clearly that the best time was after students had explored the problems.

Case 6. From Math Facts to Math Excitement

Game: How close to 100

2 dice and a 100 grid.  Multiply the two numbers and colour in the squares.  Working towards filling the grid.

The following are some of the students’ important words as they reflected on the game:

• “It challenged me to make my brain think.”
• “It was a fun way to explore math and learn.”
• “It gave me a lot of practice with multiplication.”
• “It’s a fun way to learn multiplication facts.”
• “I learned that multiplication and area are related.”
• “I know now how division, multiplication, and area are related because I can see it!”

Conclusion

When mathematics tasks are opened for different ways of seeing, different methods and pathways, and different representations, everything changes.  To summarise there are 5 suggestions that can work to open mathematics tasks and increase their potential for learning:

1. Open up the task so that there are multiple methods, pathways, and representations.
2. Include inquiry opportunities.
3. Ask the problem before teaching the method.
4. Ask a visual component and ask students how they see the mathematics.
5. Extend the task to make it lower floor and higher ceiling.
6. Ask students to convince and reason; be sceptical.

Resources:

• Youcubed
• NCTM
• NCTM Illuminations
• Balanced Assessment
• Math Forum
• Shell Center
• Dan Meyer’s resources
• Geogebra
• Video Mosaic project
• NRich
• Estimation 180
• Visual Patterns: grade K – 12
• Number Strings
• Mathalicious, grades 6 – 12; real-world lessons for middle and high school

Chapter 3 of Mathematical Mindsets

What is mathematics, really? And why do so many students either hate it or fear it – or both?  Mathematics is different from other subjects, not because it is right or wrong, as many people would say, but because it is taught in ways that are not used by other subject teachers, and people hold beliefs about mathematics that they do not hold about other subjects.

Keith Devlin, a top mathematician, has dedicated a book to this idea (mathematics is about patterns). In his book Mathematics: The Science of Patterns he writes:

As the science of abstract patterns, there is scarcely any aspect of our lives that is not affected, to a greater or lesser extent, by mathematics; for abstract patterns are the very essence of thought, of communication, of society, and of life itself. (Devlin, 1997)

An example in life:

The spider web is an amazing feat of engineering that could be constructed using calculations, but the spider intuitively uses mathematics in creating and using its own algorithm.

Mathematics exists throughout nature, art, and the world, yet most school students have not heard of the golden ratio:

https://www.mathsisfun.com/numbers/golden-ratio.html

…and do not see mathematics as the study of patterns.

the questions that drive mathematics. Solve problems and making up new ones is the essence of mathematical life.  If mathematics is conceived apart from mathematical life, of course it seems – dead

Reuben Hersh (1999) What is Mathematics, Really?

Over the years, school mathematics has become more and more disconnected from the mathematics that mathematicians use and the mathematics of life.

Four stages of mathematics:

1. Posing a question
2. Going from the real world to a mathematical model
3. Performing a calculation
4. Going from the model back to the real world, to see if the original question was answered

 

 

 

I recently (well earlier in the year) bought this book –  Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages and Innovative Teaching by Jo Boaler.  I was interested in the mindset work and also the mathematics element.  I know as a student I loved mathematics (sad I know) but as a Teacher it was often the most difficult to instil that same love of learning for mathematics.  I see it in my own children who come home and say “maths is boring”…anyway I thought that I would share this book (chapter by chapter…and only the key points)…Liz borrowed the book off me first and I know she put together some ideas she was going to try in class (maybe she will share…sorry Liz did I just dob you in 🙂 )

Anyway, starting with Chapter 2 on  the power of mistakes…

When I have told teachers that mistakes cause your brain to spark and grow, they have said, “Surely this happens only if students correct their mistake and go on to solve the problem.” But this is no the case.  In fact, Moser’s study shows us that we don’t even have to be aware we have made a mistake for brain sparks to occur…because it is a time of struggle; the brain is challenged, and this is the time when the brain grows the most.

How Can We Change the Ways Students View Mistakes?

When we teach students that mistakes are positive, it has an incredibly liberating effect on them.

The habits of successful people in general:

• Feel comfortable being wrong
• Try seemingly wild ideas
• Are open to different experiences
• Play with ideas without judging them
• Are willing to go against traditional ideas

One idea for class

Asking students who have been working on a problem and have knowingly made a mistake to share that mistake on the board.  Allows for discussions around common misconceptions and to solve the problem together.

Other resources:

• https://www.youcubed.org/think-it-up/mistakes-grow-brain/
• http://www.nctm.org/News-and-Calendar/Messages-from-the-President/Archive/Linda-M_-Gojak/The-Power-of-a-Good-Mistake/
• https://www.perts.net/
• https://www.mindsetkit.org/